Tags: "leetcode", "bit-manipulation", access_time 2-min read

Edit this post on Github

Number Complement

Created: May 5, 2020 by [lek-tin]

Last updated: May 5, 2020

Given a positive integer, output its complement number. The complement strategy is to flip the bits of its binary representation.

Example 1:

Input: 5
Output: 2
Explanation: The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.

Example 2:

Input: 1
Output: 0
Explanation: The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.

Note:

  1. The given integer is guaranteed to fit within the range of a 32-bit signed integer.
  2. You could assume no leading zero bit in the integer’s binary representation.
  3. This question is the same as 1009: https://leetcode.com/problems/complement-of-base-10-integer/

Hint:

x is some bit

0 xor x = x
1 xor x = 1 − x

Solution (bit by bit 1)

Java

class Solution {
  public int findComplement(int num) {
    int todo = num, bit = 1;
    while (todo != 0) {
      // flip current bit
      num = num ^ bit;
      // prepare for the next run
      bit = bit << 1;
      todo = todo >> 1;
    }
    return num;
  }
}

Time: O(1)
Space: O(1)

Solution (bit by bit 2)

Java

class Solution {
    public int findComplement(int num) {
        if (num == 0) return 1;

        int ans = 1;
        while (ans - 1 < num) {
            ans <<= 1;
        }
        return ans - 1 - num;
    }
}

Time: O(1)
Space: O(1)

Solution (Compute Bit Length and Construct 1-bits Bitmask)

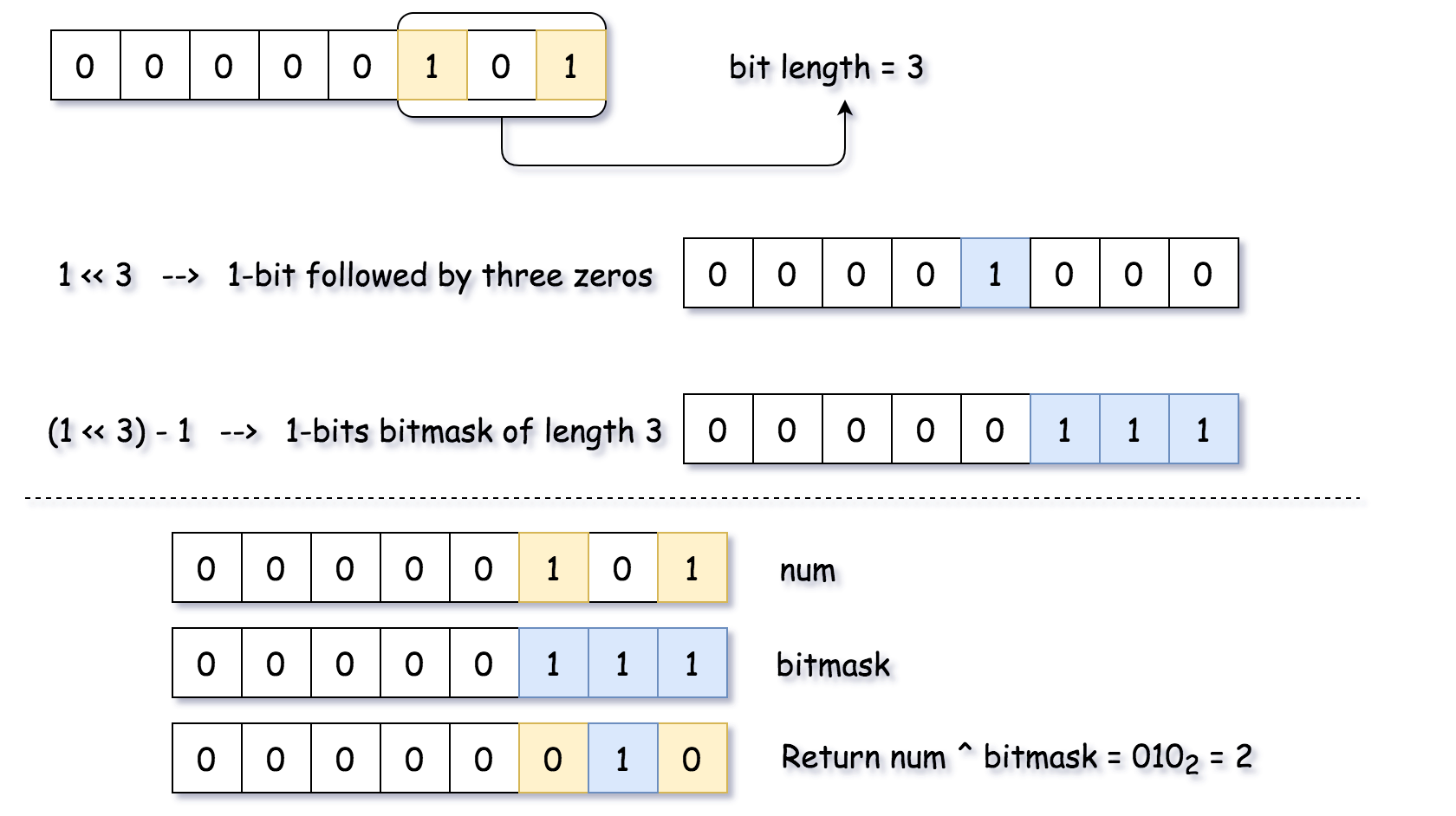Number Complement bitmask3 Java

class Solution {
    public int findComplement(int num) {
        if (num == 0) return 1;

        int n = num;
        int highest = 0;
        // n is a length of num in binary representation
        while (n > 0) {
            highest++;
            n >>= 1;
        }
        // bitmask has the same length as num and contains only ones 1...1
        int bitmask = (1 << highest) - 1;
        // flip all bits
        return bitmask ^ num;
    }
}

Time: O(1)
Space: O(1)

Solution (Built-in Functions to Construct 1-bits Bitmask)

Java

class Solution {
    public int findComplement(int num) {
        if (num == 0) return 1;
        // Integer.highestOneBit(num) return 2^k, k = the highest bit
        return num ^ ((Integer.highestOneBit(num) << 1) - 1);
    }
}

Time: O(1)
Space: O(1)