The Maze
Created: March 17, 2019 by [lek-tin]
Last updated: November 9, 2019
There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won’t stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the ball’s start position, the destination and the maze, determine whether the ball could stop at the destination.
The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.
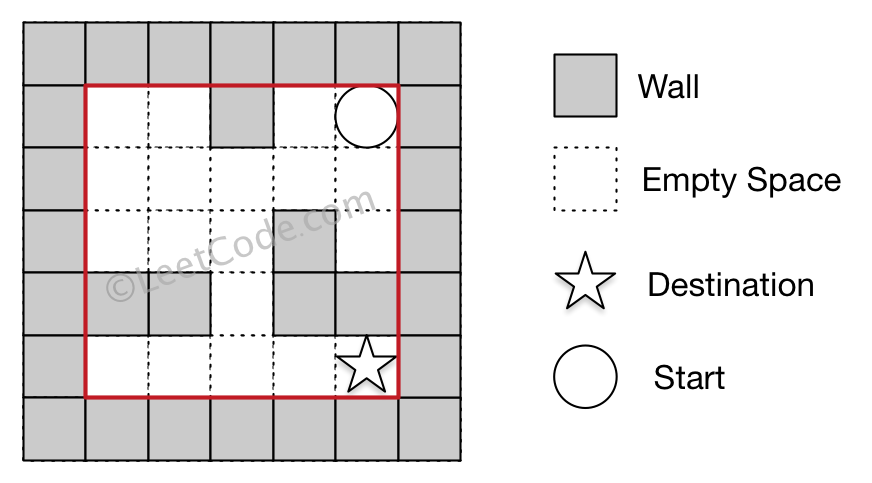
Example 1
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)
Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
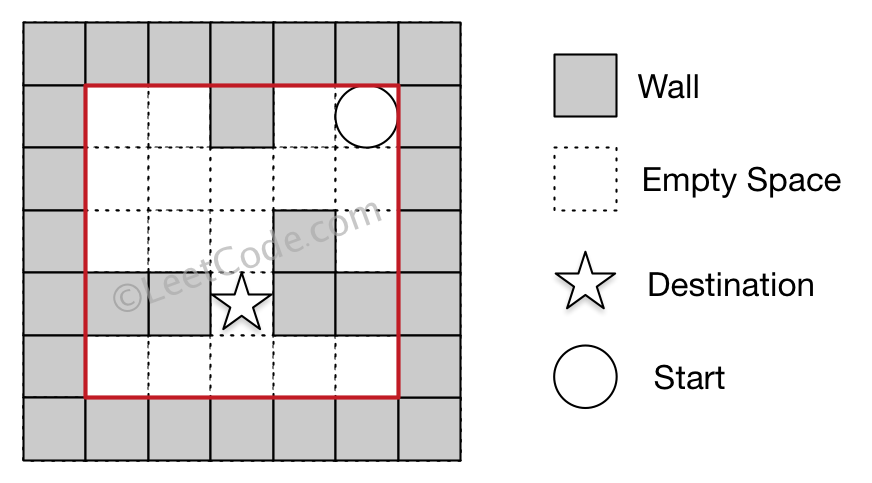
Example 2
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)
Output: false
Explanation: There is no way for the ball to stop at the destination.
Note
- There is only one ball and one destination in the maze.
- Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
- The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
- The maze contains at least 2 empty spaces, and both the width and height of the maze won’t exceed
100.
Solution
from collections import deque
class Solution:
def hasPath(self, maze: List[List[int]], start: List[int], destination: List[int]) -> bool:
n = len(maze)
m = len(maze[0])
if not maze or n == 0 or m == 0:
return False
directions = set([ (0,1), (0,-1), (1,0), (-1,0) ])
visited = [ [False for _ in range(m)] for _ in range(n)]
q = deque([])
visited[start[0]][start[1]] = True
q.append(start)
while len(q) > 0:
row, col = q.popleft()
if row == destination[0] and col == destination[1]:
return True
for dir in directions:
y, x = row, col
while 0 <= y < n and 0 <= x < m and maze[y][x] == 0:
y += dir[0]
x += dir[1]
y -= dir[0]
x -= dir[1]
# only need to check whether the stop point has been visited - not the points along the way, because a point can be visited multiple times as a along-the-path point
if not visited[y][x]:
visited[y][x] = True
q.append([y, x])
return False