Largest Divisible Subset
Created: August 29, 2019 by [lek-tin]
Last updated: August 29, 2019
Given a set of distinct positive integers, find the largest subset such that every pair (Si, Sj) of elements in this subset satisfies:
Si % Sj = 0 or Sj % Si = 0.
If there are multiple solutions, return any subset is fine.
Example 1
Input: [1,2,3]
Output: [1,2] (of course, [1,3] will also be ok)
Example 2
Input: [1,2,4,8]
Output: [1,2,4,8]
Solution
class Solution:
def largestDivisibleSubset(self, nums: List[int]) -> List[int]:
if not nums or len(nums) == 0:
return []
nums.sort()
n = len(nums)
counts = [1] * n
prev = [-1] * n
largestIndex = 0
for i in range(n):
for j in range(i):
if nums[i] % nums[j] == 0 and counts[i] < counts[j]+1:
counts[i] = counts[j] + 1
# Record the i's prev index j
prev[i] = j
# update largestIndex with the index of largest count
if counts[i] > counts[largestIndex]:
largestIndex = i
res = []
# pick numbers at each prev index
while largestIndex != -1:
res.append(nums[largestIndex])
largestIndex = prev[largestIndex]
return res
Initialization:
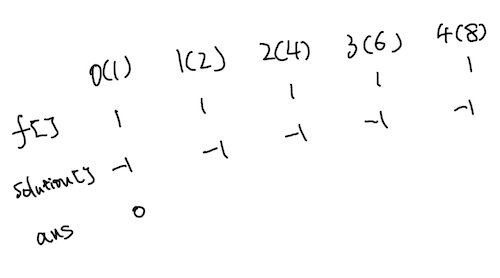
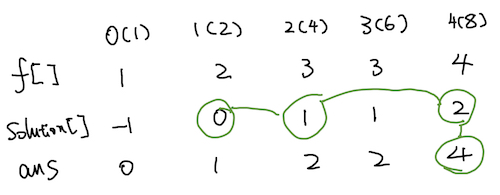
Final state