Trapping Rain Water
Created: January 26, 2019 by [lek-tin]
Last updated: January 26, 2019
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!
Example:
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Solution 1
Time: O(n)
Space: O(1)
class Solution {
public int trap(int[] height) {
int n = height.length;
int res = 0;
int left = 0;
int right = n - 1;
int leftHeight = 0;
int rightHeight = 0;
while(left <= right){
if(height[left] <= height[right]){
if(height[left] >= leftHeight) {
leftHeight = height[left];
}
else {
res += leftHeight - height[left];
}
left++;
}
else{
if(height[right] >= rightHeight) {
rightHeight = height[right];
}
else {
res += rightHeight - height[right];
}
right--;
}
}
return res;
}
}
Solution 2
Dynamic programming version
Time: O(n)
Space: O(n)
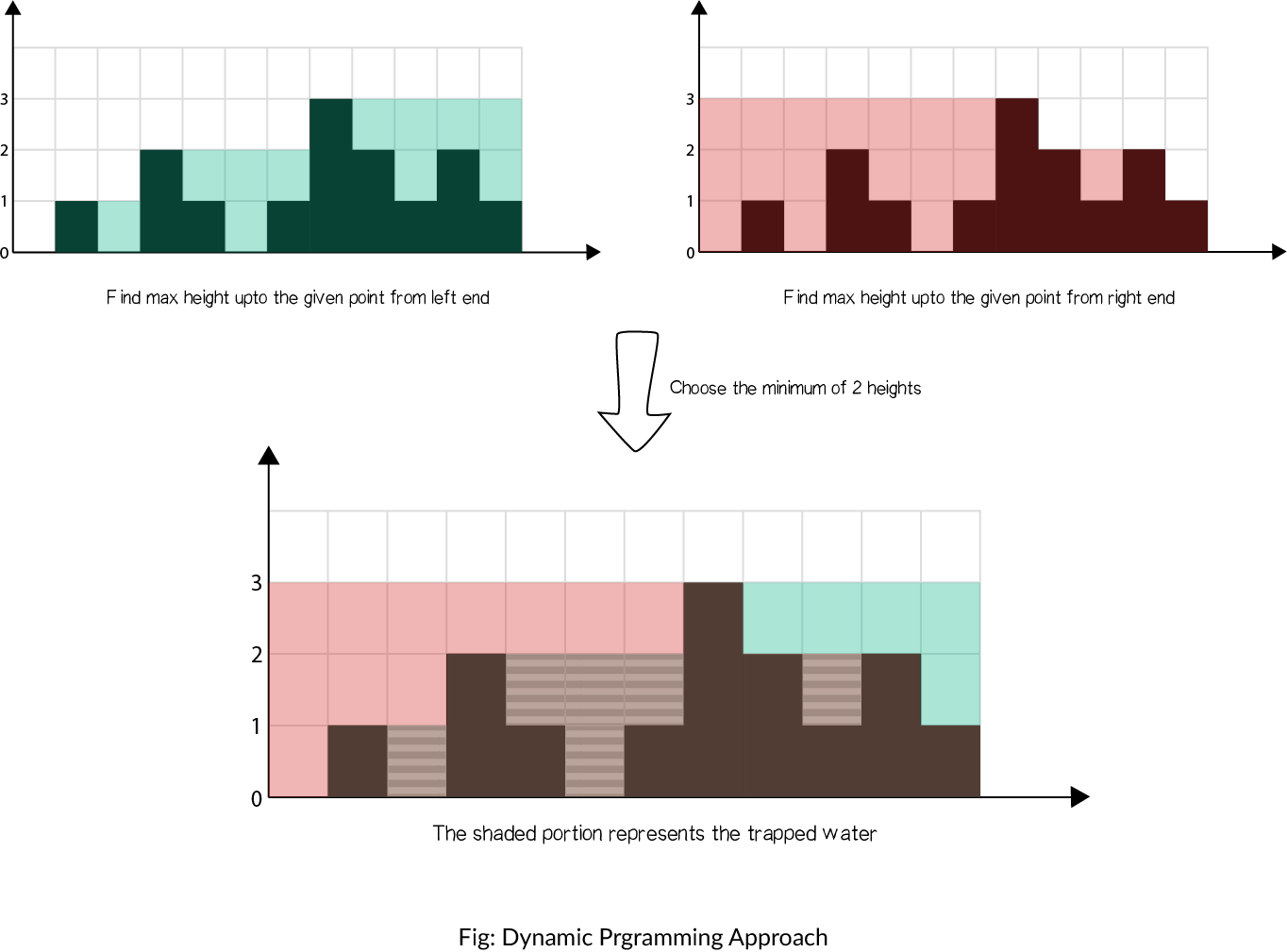
class Solution:
def trap(self, height: List[int]) -> int:
N = len(height)
if not height or N == 0:
return 0
amount = 0
left_max, right_max = [0] * N, [0] * N
# left -> right
left_max[0] = height[0]
for i in range(N-1):
left_max[i] = max(left_max[i-1], height[i])
# right <- left
right_max[-1] = height[-1]
for i in range(N-2, -1, -1):
right_max[i] = max(right_max[i+1], height[i])
# scan water at each coloum from left -> right
for i in range(1, N-1):
amount += min(left_max[i], right_max[i]) - height[i]
return amount